O software GeoGebra possui vários comandos, entre eles o comando função, que nos permite esboçar o gráfico de funções em um intervalo definido.
Sua forma base está representada abaixo:
Função( , , )
Sabe-se que uma função polinomial é da forma:
Para esboçar o gráfico da função f(x)=3x²-4x+1 no intervalo [-2,2], basta digitar Função( 3x²-4x+1, -2, 2 ) e em seguida pressionar enter.
Pronto aparecerá o gráfico como mostrado a seguir:
Sabe-se que as funções exponenciais são da forma:
A maneira mais comum com que esta função aparece é quando a = e (número de Euler), ou seja:
Digitando f(x)=exp(x) e pressionando enter temos o gráfico que representa esta função:
Como também é possível através do comando função, digitando por exemplo Função( exp(x), -5, 3 ), o qual aparecerá no intervalo [-5,3] como na imagem abaixo:
As funções trigonométricas são funções periódicas, ou seja, na sua representação gráfica as funções se caracterizam pela repetição de um padrão.
As principais funções trigonométricas são:
- Função Seno
- Função Cosseno
- Função Tangente
1- Função seno, expressa por f(x)=sen(x).
Digite Função( sen(x), 0, 2π ).
2- Função cosseno, expressa por f(x)=cos(x).
Digite Função( cos(x), 0, 2π ).
3-Função tangente, expressa por f(x)=tan(x).
Digite Função( tan(x), 0, 2π ).
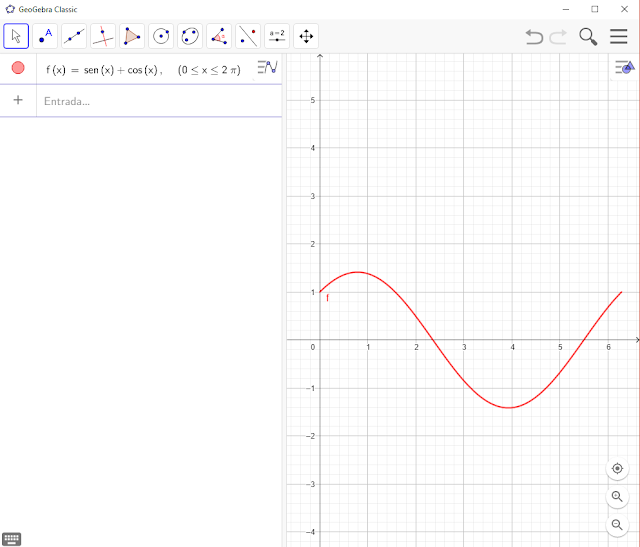
4- Esboçar o gráfico da função f(x)=sen(x)+cos(x), onde 0 ≤ x ≤ 2π
Digitando Função( sen(x)+cos(x), 0, 2π )
